
| Home | FAQs | Book Contents | Updates & News | Downloads |
There is a great tradition of learning about probability from TV Game Shows, I'm sure you are aware of the "Monty Hall Problem" and it's counter intuitive results. Here's another show which has something to tell us that I think is of direct relevance to the oil industry.

When you are first taught about statistics you are told that a probability and a value can be combined by multiplying them. So a rational person should be willing to trade $1 for a 1 in 40 chance to win $50. However, as we will see, in reality this picture is a little bit too simple.
The game show "Deal or No Deal" was originally developed in Holland, there are many minor differences between the versions shown in different territories, but they all have the same basic premise. A contestant is presented with a number of identical cases, each one contains a different amount of money and while everyone knows the amounts no one knows which case contains which prize. The contestant picks one case to keep, this is the "final case", and the remainder are selected and eliminated one at a time. Each time a case is eliminated the contestant is shown how much money was in that case, so they can keep track of the amounts that have not yet been revealed. At certain points the player is offered a "Deal", to buy the case they selected at the start, if they accept that amount that is their winnings, if they reject the "Deal" the game continues. If the contestant gets to the point where only their single case remains they win the amount of money in the final case.
In the US version of the game the amounts in the cases varies from one cent to a million dollars. The values in the various cases and the levels of the offered "Deals" are tailored to make the game interesting and to increase tension throughout the program. The game hinges on the level of "Deal" being offered. For example if the player has got to the point where only the $100 and $1,000 cases are still in play clearly a "Deal" of $100 should always be rejected, while one of $1,000 would always be accepted. The real offer will always be somewhere between these two. A simple analysis would suggest that $550 would be an appropriate offer, however in practice a contestant might accept a lower offer, preferring the certainty of a given pay-out rather than a 50:50 chance of winning even more. Of course the amount being gambled has an impact, in the above scenario some contestants might reject a $400 offer, while if the unopened boxes were for $100,000 and $1,000,000 the same player might accept an offer of $400,000.
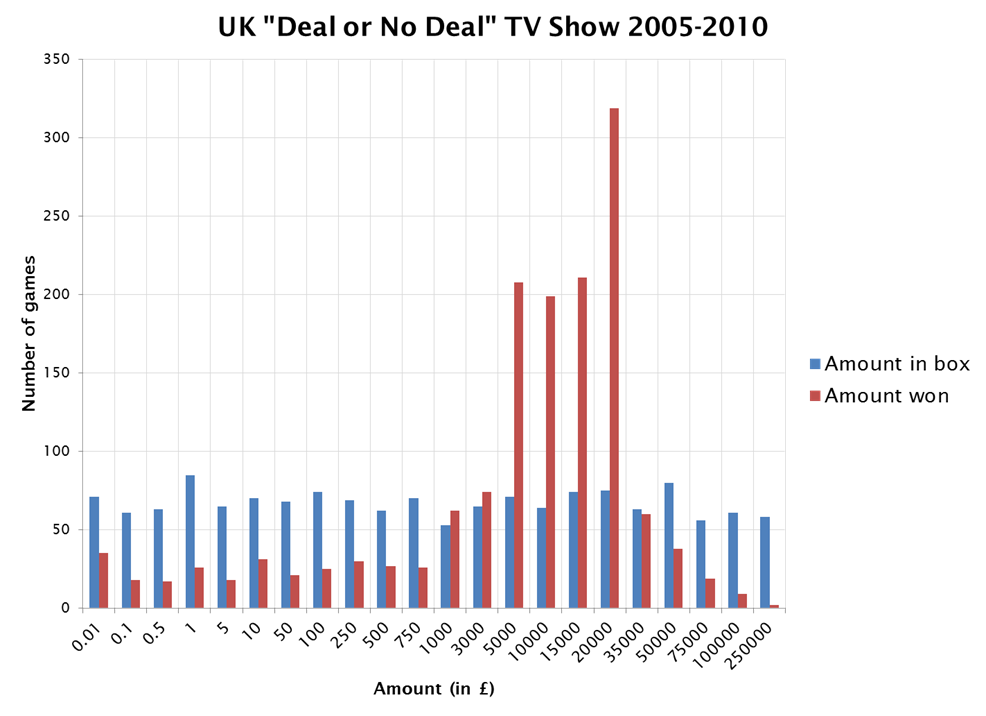
The game is presented as a competition between the off-screen "Banker" who makes the offers and the contestant. The Banker is attempting to purchase the "final case" for as low a price as possible, while the player is attempting to maximise their winnings. The actual results of more than 1,400 plays have been recorded for the UK version of the game. The results are shown in this figure, the red bars show the deals accepted by the player and the blue bars show the amounts each actually had in their "final case". Over the course of six seasons more than 74% of contestants managed to accept deals that were the same as or higher than the amount they picked. From the point of view of the players this, surely, counts as a win. So the conclusion would have to be that the Banker, therefore lost, right?
Well, no, the average value of the "final case", that is what the player would have won if they had rejected all offers, was £23,579.53 while the average actual winnings were £15,445.66. By this measure the players lost an average of more than £8,000 per game. So by this view the Banker, over the course of many games, managed to win.
So how is it that the players can have "won" three quarters of the games they played, but yet had an average pay-out that was two thirds of what was in their selected boxes? The answer is that when the players lost they lost a lot. Of the 58 occasions when the contestant initially selected the £250,000 box only two of them went on to claim that amount. The average winnings for this group were £38,293.67, so for each of these games the Banker "saved" more than £200,000, this more than made up for the £7,754 that he "over paid" for contestants that initially selected the 1p box.
The difference in view comes from the asymmetry in the game. The contestants each get to play only one single game, they have just one chance to get their winnings. In contrast the Banker plays with a longer perspective, a failure in one game can be offset against the gains that taking the same risk would yield in others. Hopefully most oil companies act more like the Banker than single shot contestants, but I can think of a few cases where oil companies have focused on short term gains to the detriment of their long term position.
Article 14 |
Articles |
RSS Feed |
Updates |
Intro |
Book Contents |
All Figures |
Refs |
Downloads |
Links |
Purchase |
Contact Us |
Article 16 |